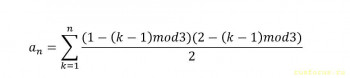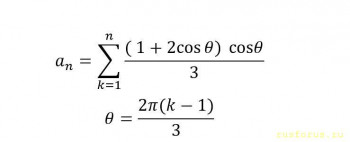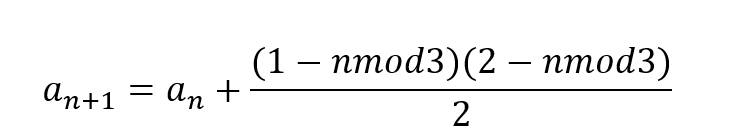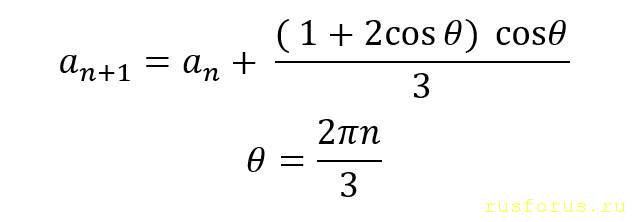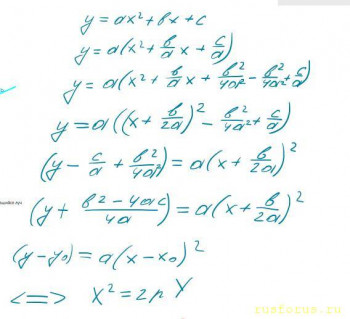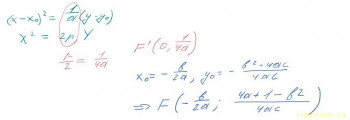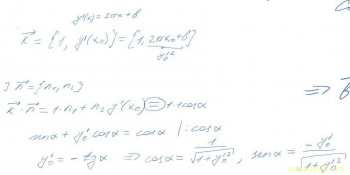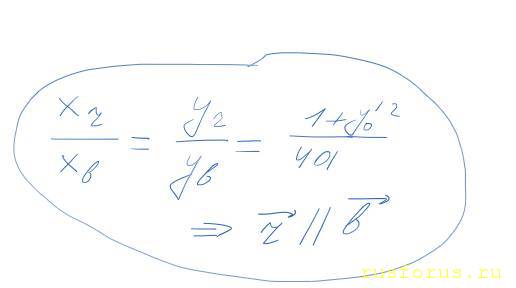самый главный енот:Сторона, наверное
Задачи не для чайников ⇐ Другие темы о русской словесности и культуре
Модератор: Penguin
-
Hex
- дьяк

- Всего сообщений: 30
- Зарегистрирован: 27.08.2016
- Образование: высшее техническое
- Профессия: + магистр менеджмента
- Откуда: Воронеж
- Возраст: 41
-
Хоровик
- заслуженный писатель форума

- Всего сообщений: 306
- Зарегистрирован: 06.05.2021
- Образование: высшее техническое
- Профессия: Безработный
- Откуда: Северная Венеция
Re: Задачи не для чайников
Отправлено спустя 35 минут 59 секунд:
Ещё такую формулу для энного члена придумал: Это если вы помните, что такое деление по модулю m
Отправлено спустя 44 минуты 14 секунд:
Ещё вот такой, гармонический, вариант придумал. Если у кого-то возникает паника от длинных математических выражений, можно сделать замену: В общем случае тригонометрический круг делится на три равные части. Здесь идея такая же, как и в предыдущем варианте: нужно сделать так, чтобы при любом n мы получали всего три возможных значения, одно из которых - единица. А остальные обнуляем. Чем-то похоже на интерполяционный полином Лагранжа (кстати, на первом курсе я вывел его сам, не зная даже о его существовании).
Возможно, существует вариант и без суммирования. Интересно поразмышлять ещё.
А что тут мучиться? a(n) = ⌈n/3⌉rusak: 02 дек 2015, 16:09 Однажды попросили написать общую формулу для последовательности
1,1,1,2,2,2,3,3,3,4,4,4,5,5,5,...
Два часа мучился, но придумал-таки! Правда, длинновато получилось. А кто из вас сумеет?
Отправлено спустя 35 минут 59 секунд:
Ещё такую формулу для энного члена придумал: Это если вы помните, что такое деление по модулю m
Отправлено спустя 44 минуты 14 секунд:
Ещё вот такой, гармонический, вариант придумал. Если у кого-то возникает паника от длинных математических выражений, можно сделать замену: В общем случае тригонометрический круг делится на три равные части. Здесь идея такая же, как и в предыдущем варианте: нужно сделать так, чтобы при любом n мы получали всего три возможных значения, одно из которых - единица. А остальные обнуляем. Чем-то похоже на интерполяционный полином Лагранжа (кстати, на первом курсе я вывел его сам, не зная даже о его существовании).
Возможно, существует вариант и без суммирования. Интересно поразмышлять ещё.
-
Хоровик
- заслуженный писатель форума

- Всего сообщений: 306
- Зарегистрирован: 06.05.2021
- Образование: высшее техническое
- Профессия: Безработный
- Откуда: Северная Венеция
-
Хоровик
- заслуженный писатель форума

- Всего сообщений: 306
- Зарегистрирован: 06.05.2021
- Образование: высшее техническое
- Профессия: Безработный
- Откуда: Северная Венеция
Re: Задачи не для чайников

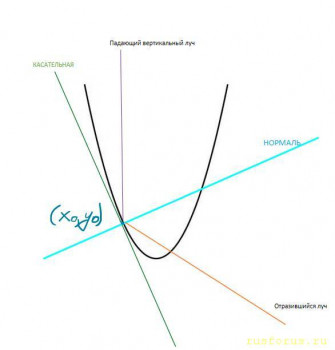
Соглашусь с тем, что парабола — она и в Африке парабола: квадратичная функция вида y = ax²+bx+c при помощи выделения полного квадрата приводится к виду X²=2pY с фокусом в точке (0, p/2) в новой СК, получившейся в результате параллельного переноса. Если забыть об определении параболы как кривой второго порядка, то что тогда будет фокусом?
Если понятие фокуса параболы неизвестно, как оно может фигурировать в условии задачи?rusak: 10 дек 2014, 18:15 ALNY, понимаете, Вы тут показали с учетом того, что известны понятия p и фокуса. То есть второе определение параболы. Я же исхожу из того, что парабола - это в общем виде
y=ax^2+bx+c
Соглашусь с тем, что парабола — она и в Африке парабола: квадратичная функция вида y = ax²+bx+c при помощи выделения полного квадрата приводится к виду X²=2pY с фокусом в точке (0, p/2) в новой СК, получившейся в результате параллельного переноса. Если забыть об определении параболы как кривой второго порядка, то что тогда будет фокусом?
Сперва нужно определить координаты фокуса для параболы y = ax²+bx+c При помощи выделения полного квадрата приводим к виду X²=2pY Выражаем p через а и находим фокус как (0, p/2) в СК с центром в (x0, y0), а затем находим координаты фокуса в исходной СК.
-
Хоровик
- заслуженный писатель форума

- Всего сообщений: 306
- Зарегистрирован: 06.05.2021
- Образование: высшее техническое
- Профессия: Безработный
- Откуда: Северная Венеция
Re: Задачи не для чайников
Теперь, собственно, само доказательство.
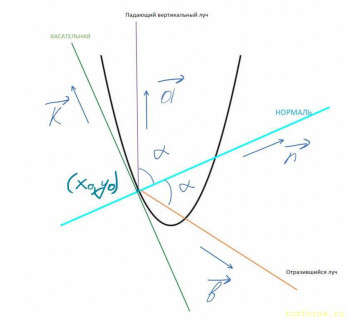
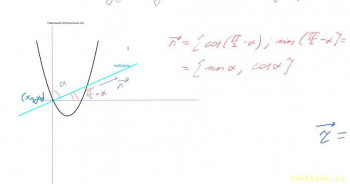
Если вас интересует именно геометрический способ, придётся решать через направляющие векторы. Найдём орты для касательной, нормали, падающего вертикального луча и отразившегося луча: Здесь я воспользовался тем фактом, что единичный вектор, образующий с положительным направлением оси Ox угол α, имеет координаты {cos α, sin α}. В таком случае мы с лёгкостью вычисляем сами тригонометрические функции от альфа при помощи скалярного произведения, а затем и координаты векторов n и b.
Если вас интересует именно геометрический способ, придётся решать через направляющие векторы. Найдём орты для касательной, нормали, падающего вертикального луча и отразившегося луча: Здесь я воспользовался тем фактом, что единичный вектор, образующий с положительным направлением оси Ox угол α, имеет координаты {cos α, sin α}. В таком случае мы с лёгкостью вычисляем сами тригонометрические функции от альфа при помощи скалярного произведения, а затем и координаты векторов n и b.
-
Хоровик
- заслуженный писатель форума

- Всего сообщений: 306
- Зарегистрирован: 06.05.2021
- Образование: высшее техническое
- Профессия: Безработный
- Откуда: Северная Венеция
Re: Задачи не для чайников
После того как нашли вектор b — направляющий вектор отразившегося луча, ищем вектор r, начало которого лежит в точке (x0, y0), а конец - в точке фокуса.
Сопоставляем векторы b и r:
О чудо! Они коллинеарны. Значит, отразившая прямая совпадает с прямой, начало которой лежит в точке отражения, а конец - в точке фокуса (т.к. обе эти прямые параллельны и проходят через общую точку (x0, y0) ). Ч.т.д.
Доказательство для параболы ветвями вниз (а < 0) проводится аналогично.
Доказательство для второй ветви параболы проводится аналогично.
Доказательство для случая, когда ордината точки падения лежит ниже фокуса, проводится аналогично, с той лишь оговоркой, что координаты векторов b и r будут выглядеть немного иначе (для a > 0 они будут направлены вверх), но орты по-прежнему останутся коллинеарны.
Доказательство для параболы ветвями вниз (а < 0) проводится аналогично.
Доказательство для второй ветви параболы проводится аналогично.
Доказательство для случая, когда ордината точки падения лежит ниже фокуса, проводится аналогично, с той лишь оговоркой, что координаты векторов b и r будут выглядеть немного иначе (для a > 0 они будут направлены вверх), но орты по-прежнему останутся коллинеарны.
-
- Похожие темы
- Ответы
- Просмотры
- Последнее сообщение
 Мобильная версия
Мобильная версия